updated:
强化学习入门笔记(二)
2020年10月26日 星期一 11时16分46秒 CST
学习内容:
周博磊强化学习纲要
第一讲
英文部分基本都为视频中原文
Difference between RL and Supervised Learning
- Sequential data as input(not i.i.d) (i.i.d:独立同分布)
- The learner is not told which actions to take, but instead must discover which actions yield the most reward by trying them
- Trial-and-error exploration(balance between exploration&exploitation)
- There is no supervisor, only a reward signal, which is also delayed(延迟奖励)
独立同分布:在概率统计理论中,如果变量序列或者其他随机变量有相同的概率分布,并且互相独立,那么这些随机变量是独立同分布。
在西瓜书中解释是:输入空间X中的所有样本服从一个隐含未知的分布,训练数据所有样本都是独立地从这个分布上采样而得。
RL特点:
试错,探索
延迟奖励
时间很重要,RL的数据是时间上关联的(sequential),不一定是iid的,而不是iid则意味着数据相关性较强,传统机器学习训练起来不稳定。
agent的行为会影响数据,如果模型差,则生成的数据也差,强化学习的问题其实就是agent和环境交互。学习极大化奖励的策略
The key elements of an RL agent: model, value, policy
第二讲 马尔科夫决策过程
Markov Chain->Markov Reward Process(MRP)->Markov Decision Process(MDP)
policy iteration
value iteration
马尔科夫链
参考笔记(一)
MRP马尔科夫奖励过程
MRP=马尔科夫链+奖励
几个概念:
Horizon: Number of maximum time steps in each episode(每一个episode的最大步数)
Return: Discounted sum of rewards from step t to horizon
state value function Vt(s) for MRP: Expected return from t in state s (Present value of future rewards)
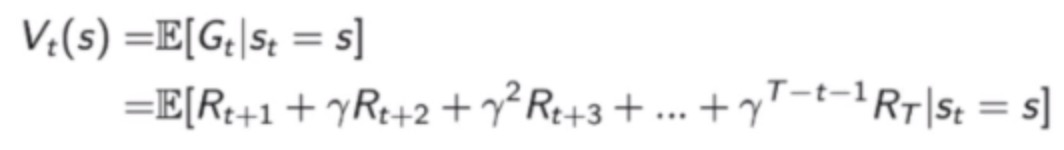
关于式中γ,笔记(一)中有记述,可参照阅读
Bellman equation
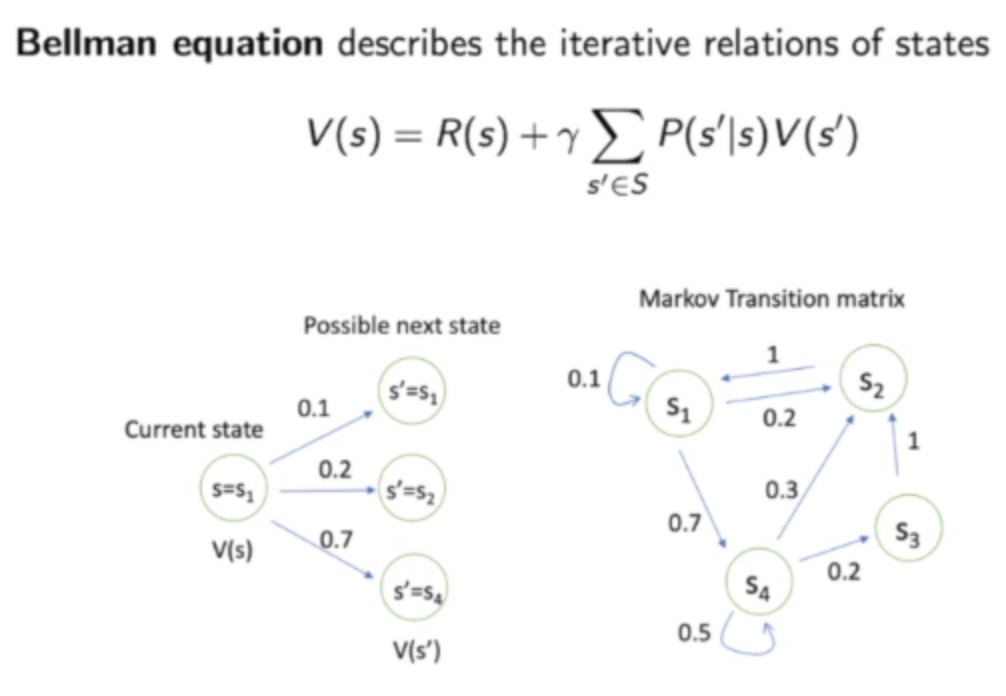
s’表示未来状态,P(s’|s)代表转移概率

对于大型的MRP的价值向量V有以下计算方法:
DP、Monte-Carlo evaluation、temporal-Difference learning
MDP马尔科夫决策过程
本节要点:MDP概念、policy evaluation on MDP、policy iteration、value iteration
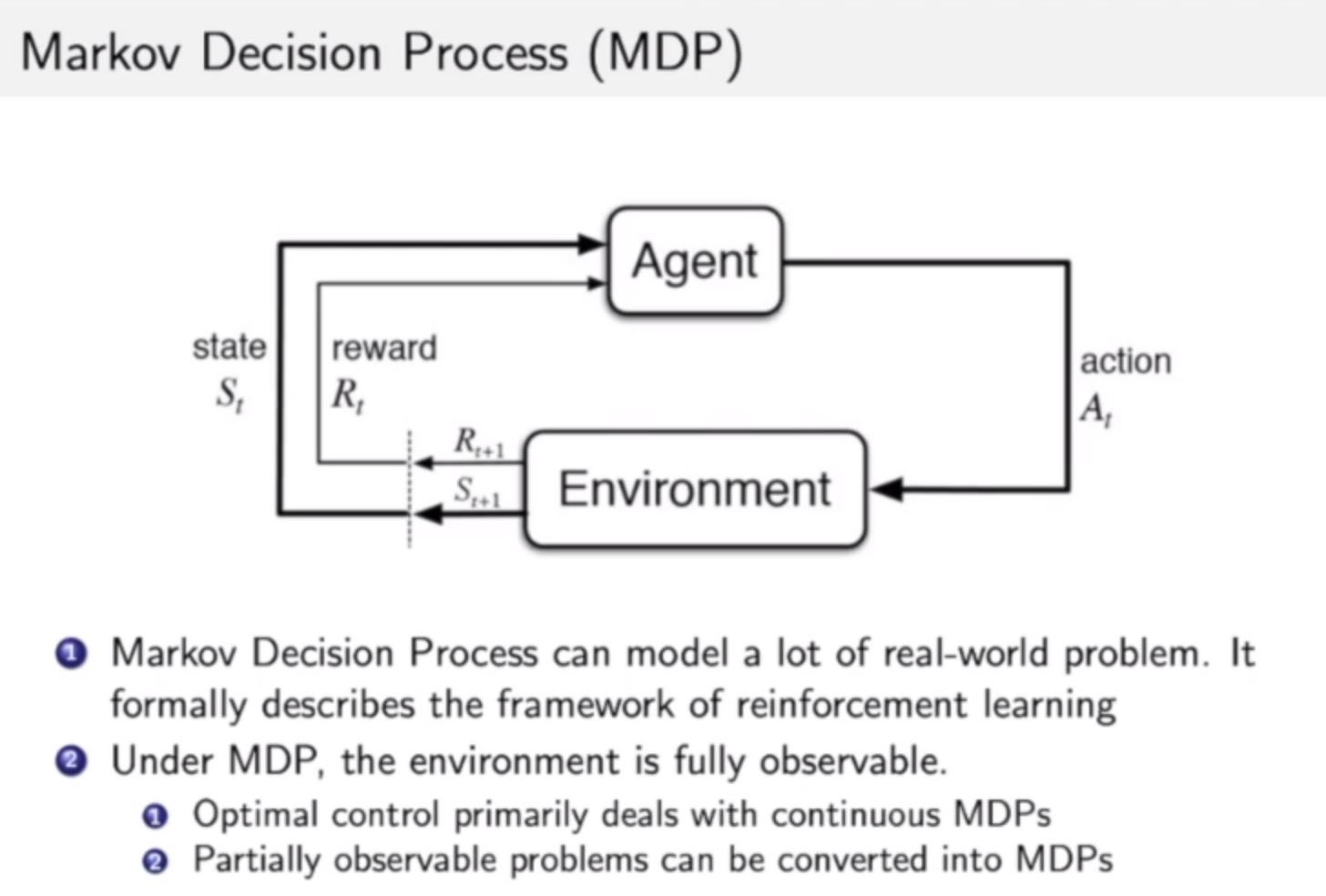
相比马尔科夫奖励过程,MDP多了action(agent决定),多了决策的问题。根据当前状态和在该状态下采取的行为,会有不同的奖励。
价值函数参考笔记(一)和report(1),详细推导最好可以完全弄懂(目前未解决)
policy evaluation
Objective: Evaluate the value of state given a policy π: compute Vπ(s).
Output: the value function under policy Vπ
Solution: iteration on Bellman expectation backup
Algorithm: Synchronous backup(转换成DP的迭代,反复迭代直到收敛,收敛时就是当前t的价值函数)
Convergence: V1->V2->…->Vπ
例子:https://cs.stanford.edu/people/karpathy/reinforcejs/gridworld_dp.html
policy evaluation的形式是,给定一个MDP,和对应的策略,可以得到马尔可夫链上value function的过程。MDP可以有最佳的价值函数(最佳指的是找到一个决策π使得价值函数上每个值为最大,可能有多个最佳决策)
寻找最优策略可以通过对Q函数进行极大化来解决。(argmax Q*(s,a))
Decision Making in MDP

DP是解MDP的predict和control问题的有效方式
寻找最优策略的具体方法:policy iteration & value iteration(都是DP)
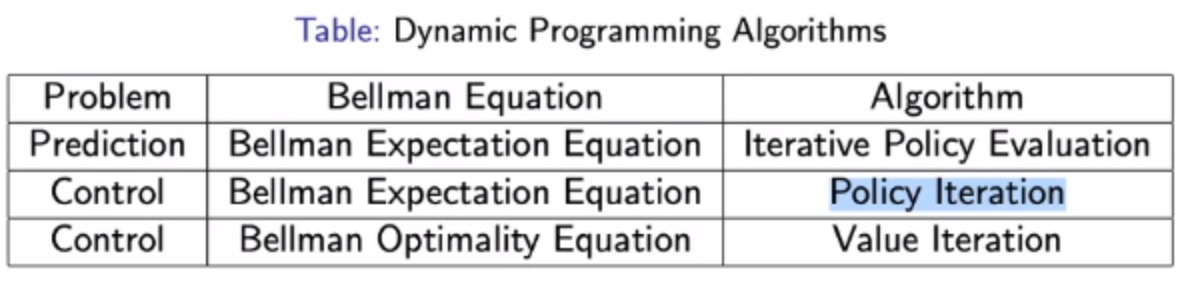
policy iteration
step:Evaluate policy π (计算当前π的价值函数v,然后推算q) -> Improve the policy(对q函数做贪心,即argmax)
反复以上过程,迭代至收敛。
value iteration
step:finding optimal value function + one policy extraction